2022. 7. 26. 03:09ㆍMathematics for CG
이전 글에서 선형 결합과 선형 독립, 기저에 대해 알아보았다.
이제 선형 변환(linear transformation)에 대해 알아보자.
변환(transformation)이란, n-차원의 공간을 m-차원의 공간으로 사상(mapping)하는 함수를 말하며,
다음과 같이 표기한다.
T:Rn↦Rm
예를 들어, 다음 함수 f(x,y)는 R2에서 R으로 사상하는 함수이다.
f(x,y)=x2+y2
체 F 위의 벡터 공간 V에서 W로 사상하는 선형 변환 T는 다음 두 가지의 중요한 성질을 만족한다.
- T(v0+v1)=T(v0)+T(v1)(v0,v1∈V)
- T(av)=aT(v)(v∈V,a∈F)
따라서 어떤 변환 T가 선형 변환인지 확인하기 위해서는 다음 식을 만족하는지 확인해보면 된다.
T(ax+y)=aT(x)+T(y)
예를 들어, T(x)=kx는 선형 변환이다.
T(ax+y)=k(ax+y)=akx+ky=aT(x)+T(y)
하지만, T(x)=k0x+k1는 선형 변환이 아니다.
T(ax+y)=k0(ax+y)+k1=ak0x+(k0y+k1)=ak0x+T(y)≠aT(x)+T(y)
이제 선형 결합으로 생성된 어떤 벡터 v에 선형 변환을 적용해보자.
T(v)=T(x0v0+x1v1+···+xn−1vn−1)
선형 변환은 T(ax+y)=aT(x)+T(y) 방정식을 만족시키므로 위 선형 결합에 적용된 선형 변환을
다음과 같이 다시 쓸 수 있다.
T(v)=x0T(v0)+x1T(v1)+···+xn−1T(vn−1)
이 식은 변환된 벡터 T(v)가 변환된 기저들 T(v0),...,T(vn−1)의 선형 결합으로 나타낼 수 있다는 것을 보여준다.
선형 변환 T는 벡터 공간 V에서 W로 사상하므로 변환된 기저 벡터 T(vi)는 W의 기저들 w0,...,wn−1의 선형 결합으로 나타낼 수 있을 것이다.
T(vi)=a0,iw0+a1,iw1+···+am−1,iwm−1
위 식을 T(v)를 구하는 식에 대입해보자.
T(v)=x0(a0,0w0+···+am−1,0wm−1)+x1(a0,1w0+···+am−1,1wm−1)+x2(a0,2w0+···+am−1,2wm−1)···+xn−1(a0,m−1w0+···+am−1,m−1wm−1)
위 식을 기저 w 중심으로 전개하면 다음과 같다.
T(v)=(x0a0,0+···+xn−1a0,n−1)∗w0+(x0a1,0+···+xn−1a1,n−1)∗w1+(x0a2,0+···+xn−1a2,n−1)∗w2···+(x0am−1,0+···+xn−1am−1,n−1)∗wm−1
bi를 다음과 같이 정의하면,
bi=x0ai,0+x1ai,1+···+xn−1ai,n−1
이제 T(v)를 다음과 같이 쓸 수 있다.
T(v)=b0w0+b1w1+···+bm−1wm−1
즉, 기저 wi의 선형 결합 계수 bi만 찾아내면 벡터를 선형 변환한 결과를 얻을 수 있다.
선형 변환의 장점은 선형 변환을 행렬로 표현할 수 있다는 것이다. 행렬 표현의 장점은 행렬로 표현된 여러 변환을 합성하여 하나의 행렬로 나타낼 수 있으며, 행렬은 GPU에 의해 빠르게 계산될 수 있다.
이제 선형 변환을 행렬로 나타내보자.

행렬 M의 열벡터를 보면 벡터 공간 W에서의 T(vi)의 선형 결합 계수인 것을 알 수 있다.

즉, 벡터 공간 V의 기저(vi)들이 선형 변환을 통해 벡터 공간 W에서 어디에 사상되는지 알 수 있으면 행렬 M을 만들 수 있고, 행렬 M과 벡터 공간 V에 있는 벡터 x를 곱하면 벡터 공간 W에서 벡터 x가 어디에 사상되는지 알 수 있다.
대표적인 선형 변환 중 하나인 R3 벡터 공간에서의 크기 변환을 예로 들어보자.
크기 변환은 각 축으로 sx,sy,sz 만큼 크기를 곱하는 변환으로, 같은 벡터 공간으로 사상하는 선형 변환
(R3↦R3)이다. (같은 벡터 공간으로 사상하는 선형 변환을 linear operator라 한다.)
T(v)=(sxvx,syvy,szvz)=sxvx+syvy+szvz
이 함수를 통해 표준 기저 벡터 i=(1,0,0),j=(0,1,0),k=(0,0,1)는 다음과 같이 변환된다.
T(i)=(sx,0,0)=sxi+0j+0kT(j)=(0,sy,0)=0i+syj+0kT(k)=(0,0,sz)=0i+0j+szk
변환된 기저들의 선형 결합 계수들을 열벡터로 만들어서 행렬 M을 만들면 다음과 같다.

이제 이 행렬을 통해 모든 R3의 벡터를 변환할 수 있다.
마지막으로 기저 변환(change of basis)에 대해 알아보자.
기저 변환은 어떤 기저 v에 대해 표현된 좌표들을 다른 기저 w에 대해 표현된 좌표들로 변환하는 작업을 말하는데, 컴퓨터 그래픽스에서는 월드 → 카메라 좌표계 변환과 같이 한 좌표계의 좌표들을 다른 좌표계로 표현하는 일이 흔하기 때문에 매우 중요한 개념이라 할 수 있다.
두 기저 {v0,v1,...,vn−1}와 {u0,u1,...,un−1}와 벡터 v=x0v0+x1v1+···+xn−1vn−1가 있다고 해보자. 우리가 알고 싶은 것은 기저 vi에 대한 좌표 (x0,x1,...,xn−1)를 기저 ui에 대한 좌표로 변환하는 행렬 M이다.

행렬 M을 구하는 과정은 선형 변환을 행렬로 변환하는 과정과 다르지 않은데, 기저 변환은 선형 변환이기 때문이다.
선형 변환은 변환된 기저 벡터들이 어느 좌표에 놓일지만 알면 나머지 벡터들이 놓일 좌표를 알 수 있다고 했다. 따라서 기저 vi를 기저 ui로 나타내보자.
vi=a0,iu0+a1,iu1+···+an−1,iun−1
벡터 v=x0v0+x1v1+···+xn−1vn−1에 위에서 구한 vi를 치환한다.

이제 벡터 v를 다음과 같이 벡터와 행렬의 곱으로 나타낼 수 있으며,

기저 vi에 대한 좌표에서 ui에 대한 좌표로 변환하는 기저 변환 행렬 M도 알 수 있다.
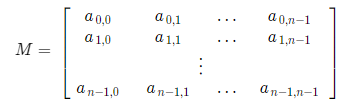
예로, 벡터 v=2∗(1,0)+3∗(1,2)를 기저 변환을 통해 표준 기저 벡터로 나타내보자.
먼저, 변환 전의 기저 (1,0),(1,2)를 표준 기저 벡터 (1,0),(0,1)로 나타낸다.
(1,0)=1∗(1,0)+0∗(0,1)(1,2)=1∗(1,0)+2∗(0,1)
각 선형 결합의 계수들을 행렬의 열벡터로 나타낸다.

(2,3)을 행렬 M에 곱하면 표준 기저 벡터에서의 좌표를 얻을 수 있다.
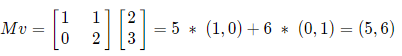
기저 변환을 통해 변환된 기저들은 여전히 선형 독립을 유지한다. 하지만, 모든 선형 변환이 선형 독립을 유지 시키지는 않기 때문에 기저 변환이 아닌 선형 변환도 있다. 즉, 기저 변환은 선형 변환이지만 모든 선형 변환이 기저 변환인 것은 아니다.
또한, 역행렬이 없을 수 있는 선형 변환과는 다르게 기저 변환은 선형 독립을 유지하기 때문에 항상 역행렬이 존재하며, 이 말은 어떤 벡터에 적용한 기저 변환을 되돌릴 수 있다는 뜻이다.
바로 위 예제에서 구한 행렬 M의 역행렬을 구해보자.

좌표 (5,6)은 기저 변환 행렬 M에 (2,3)을 곱해서 나온 결과였다.
이제 (5,6)에 역행렬 M−1을 곱해보면 기저 변환 전 좌표 (2,3)이 나오는 것을 확인할 수 있다.
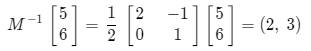
다음 글에서는 점(Point)과 아핀 공간(Affine Space)에 대해 알아보겠다.
'Mathematics for CG' 카테고리의 다른 글
| 6. 아핀 변환 (Affine Transformation) (0) | 2022.08.04 |
|---|---|
| 5. 아핀 결합(Affine Combination) (0) | 2022.08.02 |
| 4. 점(Point)과 아핀 공간(Affine Space) (0) | 2022.08.02 |
| 2. 선형 결합(Linear Combination)과 선형 독립(Linear Independence) (0) | 2022.07.24 |
| 1. 벡터(Vector)와 벡터 공간(Vector Space) (0) | 2022.07.24 |