2022. 7. 24. 23:15ㆍMathematics for CG
이전 글에서 벡터 공간은 벡터의 덧셈과 스칼라 곱에대해 닫혀있다는 것을 알았다.
이제 이 성질을 이용하면 벡터의 덧셈과 스칼라 곱을 조합하여 새로운 벡터를 생성할 수 있다.
임의의 벡터 집합 $ S = \{v_0, ...., v_{n-1}\} $을 가정해보자.
집합 S에 있는 벡터들($v_0, ..., v_{n-1}$)과 임의의 실수 스칼라($a_0, ..., a_{n-1}$)들을 조합하여 다음과 같이 새로운 벡터를 생성할 수 있다.
$$ v = a_0v_0 + a_1v_1 + ··· + a_{n-1}v_{n-1} $$
이것을 집합 $S$에 있는 벡터들의 선형 결합(linear combination)이라고 한다.
이렇게 선형 결합으로 임의의 스칼라들을 조합하면 수많은 벡터들을 만들어낼 수 있을 것이고, 이 벡터들의 집합은 벡터 공간을 형성하며, 집합 $S$가 벡터 공간을 생성(span) 한다고 한다.
예를 들어, $v_0 = (1, 0), v_1 = (0, 1)$ 두 벡터를 선형 결합하면 다음과 같다.
$$ v = a_0v_0 + a_1v_1 $$
$$ v = a_0 * (1, 0) + a_1 * (0, 1) $$
이 선형 결합이 생성하는 벡터 공간은 2차원 평면($\mathbb{R^2}$)인 것을 알 수 있다.
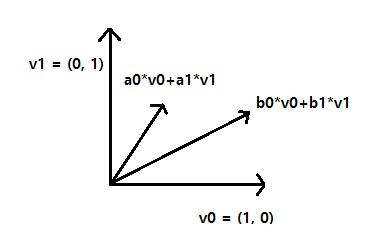
그럼 여기에 벡터 $v_2 = (2, 0)$를 하나 더 추가하여 선형 결합을 구성해보자.
$$ v = a_0v_0 + a_1v_1 + a_2v_2 $$
$$ v = a_0 * (1, 0) + a_1 * (0, 1) + a_2 * (2, 0) $$
이 선형 결합 역시 2차원 평면($\mathbb{R^2}$)을 생성함을 알 수 있다.
$$ span(\{v_0, v_1\}) = span(\{v_0, v_1, v_2\}) $$
이렇게 어떤 집합 $S = \{v_0, v_1, ..., v_{n-1}\}$에 속한 벡터들 중에서 한 벡터를 빼도 같은 벡터 공간이 생성되는 경우, 다른 관점으로는 집합 $S$에 있는 한 벡터가 나머지 벡터들의 선형 결합으로 만들어질 수 있는 경우, 집합 $S$를 선형 종속(linearly dependent)이라고 한다.
$$ a_0v_0 + a_1v_1 + ··· + a_{n-2}v_{n-2} + a_{n-1}v_{n-1} = 0 $$
즉, 위 식에서 집합 $S$가 선형 종속이면 한 벡터가 다른 벡터들의 선형 결합으로 표현될 수 있기 때문에 스칼라 $a_i$중 적어도 하나는 0이 아닐 것이다.
반대로 모든 스칼라 $a_i$의 값이 0이면 집합 $S$에 있는 어느 벡터도 나머지 벡터들의 선형 결합으로 표현될 수 없으며, 집합 $S$를 선형 독립(linearly independent)이라고 한다.
어떤 벡터 공간 $V$를 생성하는 선형 독립 집합 $S$의 벡터들을 기저 벡터(basis vector)라고 한다. 벡터 공간에는 무수히 많은 기저 벡터들의 집합이 존재하는데, 예를 들어 $\mathbb{R^2}$ 공간을 생성하는 기저벡터 집합들은 다음과 같은 것들이 있다.
$$S_0 = \{ (1,0), (0,1) \}$$
$$S_1 = \{ (2,0), (0,1) \}$$
$$S_2 = \{ (1,0), (0,2) \}$$
특히 직교좌표계 축 양의 방향으로 크기(norm)가 1인 기저 벡터들을 표준 기저 벡터(standard basis vector)라고 부르며, 우리가 흔히 사용하는 $i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1)$가 대표적인 표준 기저 벡터이다.
$\mathbb{R^n}$ 공간을 생성하는 기저 벡터 집합 $S$는 항상 $n$개의 원소만이 포함되어야 하는데, 이 집합에 원소가 하나 더 많은 경우 $\mathbb{R^n}$ 공간은 생성하지만 선형 종속인 집합이 되며, 원소가 하나 더 적은 경우 $\mathbb{R^n}$ 공간을 생성할 수 없게된다.
$$S_0 = \{ (1,0), (0,1), (2,0) \} \; ( span(S_0) = \mathbb{R^2}, 선형 종속 )$$
$$S_1 = \{ (1,0) \} \; ( span(S_1) \neq \mathbb{R^2} ) $$
즉, $\mathbb{R^n}$ 공간을 생성하는 집합의 기저 벡터들의 개수는 항상 $n$개이며, 이것은 벡터 공간의 차원(dimension)과 같다.
기저 벡터들은 중요한 특징이 있는데, 기저 벡터들의 선형 결합으로 생성된 벡터는 고유하다는 것이다. 이 말은, 벡터 $v$를 생성하기 위해 사용된 기저 벡터들의 선형 결합 계수가 고유하다는 의미이므로 v를 다음과 같이 n-tuple 형태로 나타낼 수 있다.
$$ v = a_0v_0 + a_1v_1 + ··· + a_{n-1}v_{n-1} $$
$$ v = (a_0, a_1, ..., a_{n-1}) $$
주의 할 점은 $(1,0)$과 $(0,1)$이 다르듯이 n-tuple 요소의 순서가 중요하며, 같은 벡터를 생성하더라도 사용된 기저 벡터 집합에 따라서 n-tuple의 값이 달라질 수 있다는 것이다.
예를 들어 기저 $A = \{ (1, 0), (0, 1) \}$와 기저 $B = \{ (1, 0), (1, 1) \}$가 있으면,
$$(3, 2) = 3 * (1, 0) + 2 * (0, 1) = (3, 2)_A$$
$$(3, 2) = 1 * (1, 0) + 2 * (1, 1) = (1, 2)_B$$
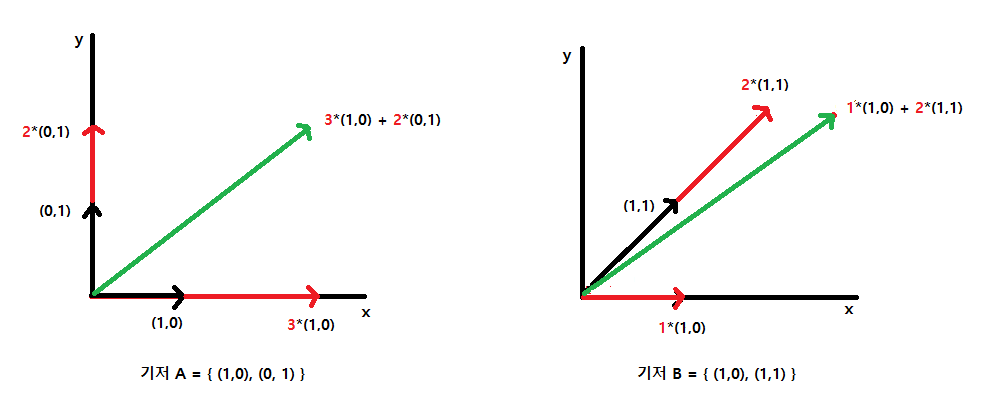
위에서 보는 것 처럼 직교 좌표계의 $(3, 2)$라는 벡터를 표현하기 위해 필요한 순서쌍이 기저에 따라 달라지는 것을 알 수 있다. 하지만, 따로 표기나 언급이 없으면 n-tuple은 표준 기저 벡터를 기준으로 한다.
이제 $\mathbb{R^3}$ 공간에서 표준 기저 벡터로 생성된 두 벡터를 더해보자.
$$ u = x_0i + y_0j + z_0k \;\; w = x_1i + y_1j + z_1k $$
$$ u + w = (x_0 + x_1)i + (y_0 + y_1)j + (z_0 + z_1)k $$
$$ u + w = (x_0 + x_1, y_0 + y_1, z_0 + z_1) $$
즉, $u = (x_0, y_0, z_0)$, $w = (x_1, y_1, z_1)$의 각 요소끼리 더한 결과와 같다.
이제 스칼라 곱을 해보자.
$$ u = xi + yj + zk $$
$$ au = (ax)i + (ay)j + (az)k $$
$$ au = a(x, y, z) = (ax, ay, az) $$
즉, $u = (x, y, z)$의 각 요소에 스칼라 $a$를 곱해준 것과 같다.
이러한 결과는 선형 결합을 통한 벡터의 표현과 과 n-tuple을 통한 벡터의 표현을 교환하여(interchangeably) 사용할 수 있다는 것을 보여준다.
다음 글에서는 컴퓨터 그래픽스에서 아주 중요한 개념인 선형 변환(Linear Transformation)에 대해 알아보겠다.
'Mathematics for CG' 카테고리의 다른 글
| 6. 아핀 변환 (Affine Transformation) (0) | 2022.08.04 |
|---|---|
| 5. 아핀 결합(Affine Combination) (0) | 2022.08.02 |
| 4. 점(Point)과 아핀 공간(Affine Space) (0) | 2022.08.02 |
| 3. 선형 변환(Linear Transformation), 기저 변환(Change of Basis) (1) | 2022.07.26 |
| 1. 벡터(Vector)와 벡터 공간(Vector Space) (0) | 2022.07.24 |