7. 동차 좌표계(Homogeneous Coordinates)와 아핀 변환 행렬(Affine Transformation Matrix)
이전 글에서 아핀 변환에 대해 알아보았는데, 마지막 부분에 해당 글에서 소개한 아핀 변환에 대한 정보로는 컴퓨터 그래픽스에서 실용성이 떨어진다고 언급하였다. 이번 글에서는 그 이유와, 해결 방법인 동차 좌표계(Homogeneous Coordinates)에 대해 알아보자.
선형 변환의 장점은 행렬로 나타낸 여러 선형 변환들을 합성하여 하나의 행렬로 나타낼 수 있으며, 이로 인해 각 벡터에 모든 선형 변환을 차례로 적용하는게 아니라, 합성된 선형 변환 하나만 곱해주면 되므로 계산이 훨씬 줄어든다.
L0(x)=M0xL1(x)=M1x⋮Ln−1(x)=Mn−1x
(Ln−1∘⋯∘L1∘L0)(x)=(Mn−1…M1M0)x
이제 아핀 변환에 대해 상기해보자.
아핀 변환은 선형 변환과 평행 이동의 조합으로 다음과 같이 나타낼 수 있음을 알고있다.
A(x)=L(x)+t
선형 변환은 행렬로 표현이 가능하므로, 아핀 변환을 다음과 같이 행렬과 벡터의 합으로 나타내보자.
A(x)=Mx+t
이제 선형 변환과 같이, 아핀 변환을 합성해보자.
A0(x)=M0x+t0A1(x)=M1x+t1(A1∘A0)(x)=M1(M0x+t0)+t1=M1M0x+M1t0+t1
몇 번을 합성해도 항이 하나였던 선형 변환과는 달리, 아핀 변환은 위와 같이 합성할수록 항이 늘어나고 식이 복잡해지며, 변환 횟수가 늘어남에 따라 계산량이 상당히 많아진다.
그럼 아핀 변환을 선형 변환으로 만들어 줄 수 없을까?
아핀 변환이 선형 변환이 된다면 회전, 크기, 밀기 변환 등의 선형 변환과 더불어 평행 이동까지 행렬로 표현할 수 있을테니 위의 문제는 해결될테니 말이다.
이 질문에 대한 답이 바로 동차 좌표계이다.
n차원의 좌표 (x0,x1,...,xn−1)를 n+1차원의 좌표 (wx0,wx1,...,wxn−1,w)로 표현하는 방법을 동차 좌표계(Homogeneous Coordinates)라고 한다. 동차 좌표는 w로 나누면 (x0,x1,...,xn−1,1)가 되는 것을 볼 수 있는데, 이 좌표에서 마지막 1을 제외해서 직교 좌표로 변환하면 (wx0,wx1,...,wxn−1,w) 좌표의 점들 또는 이 점들이 형성하는 선이 직교 좌표 (x0,x1,...,xn−1)에 대응 된다고 볼 수 있다.

w는 0이 아닌 어떤 값도 될 수 있지만, w=1인 경우 아래에서 소개할 아핀 변환 행렬을 곱해도 결과가 항상 (x′0,x′1,...,x′n−1,1)의 형태이기 때문에 w로 나눌 필요 없이 변환된 n차원 직교 좌표를 바로 얻을 수 있다. 하지만, 나중에 다룰 투영 변환(Projection Transformation)은 w의 값을 1로 반드시 보존하는 것은 아니라는 것만 기억하자.
이제 동차 좌표계란 개념이 아핀 변환을 어떻게 선형 변환으로 만들어 줄 수 있는지 알아보자.
먼저, 2차원 평면에서 다음과 같은 점 집합을 평행 이동 시킨다고 해보자.

이 점 집합을 2차원에서 평행 이동 시키기 위해서는 아핀 변환을 이용해야하므로 선형 변환으로는 평행 이동 시킬 수 없다. 여기서 차원을 하나 증가시켜서 3차원 z=1에 위 평면을 끼워 넣으면 다음과 같을 것이다.

이 상태에서 z=1 평면에 있는 점 집합 (x,y,1)을 xy평면에 투영하면 다음과 같은 모형을 예상할 수 있다.

이 상태에서 z=1 평면에 있는 점 집합 (x,y,1)를 x축 또는 y축으로 평행 이동 시켜보자.

평행 이동 전, 후의 모양을 보면 3차원 공간에서 선형 변환 중 하나인 전단 변환(밀기 변환, Shear Transformation)이 적용된 것을 알 수 있다. 즉, 3차원 공간에서 (x,y,1) 좌표의 점들을 전단 변환하면 이 점들이 (x′,y′,1) 좌표로 평행 이동 된다는 것이다.
행렬을 통해 이 과정을 확인해보자.
z축을 고정시키고 x,y축을 전단 시키는 3차원 전단 변환 행렬 M은 다음과 같으며, a,b는 전단 계수(Shearing Factor)이다.
M=[10a01b001]
이 행렬에 (x,y,1) 좌표의 점들을 곱해보자.
$$ \begin{bmatrix}x' \\ y' \\ 1 \end{bmatrix} =
[10a01b001]
[xy1] =(x + a, \;y + b, \;1) $$
(x,y,1)에서 (x+a,y+b,1)로 점들이 평행 이동된 것을 볼 수 있다.
동차 좌표계를 통해 2차원의 평행 이동을 3차원의 밀기 변환 행렬로 표현이 가능함을 확인했다. 2차원 평행 이동과 더불어, 2차원의 모든 선형 변환들 또한 3차원의 선형 변환 행렬로 나타낼 수 있다. 이것을 일반화해서, n차원 점들의 아핀 변환은 n+1차원의 선형 변환 행렬로 나타낼 수 있는데, 이 (n+1)×(n+1) 행렬을 아핀 변환 행렬(Affine Transformation Matrix)라고 한다. 아핀 변환 행렬은 다음과 같은 형태를 띄며, L은 n×n의 선형 변환 행렬이며, t는 평행 이동을 위한 n차원의 열벡터(n×1)이다.
A=[Lt01]
예를 들어, 30도 회전 후 (−1,2)만큼 평행 이동하는 행렬은 다음과 같다.
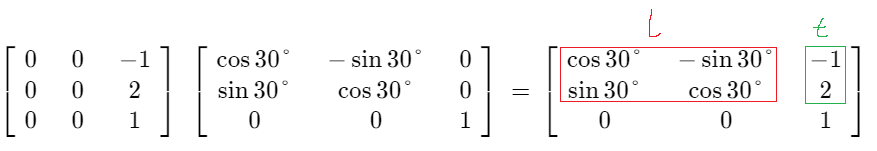
지금까지 동차 좌표계에 대해서 알아보았다.
이제 행렬로 평행 이동을 표현할 수 있게 되었으니, 다음 글에서는 프레임 (O,α)을 프레임 (O′,β)로 변환하는 변환에 대해서 알아보겠다. (프레임은 좌표를 나타내기 위해 기준이 되는 원점과 기저 쌍을 말한다.)
